本文最后更新于:2022年3月6日 晚上
可持久化线段树学习笔记
前言
之前写到一题区间第k大相关的题,可惜不会主席树,就现在学了一学
前置知识
1、线段树
2、离散化
正式开始
可持久化线段树是维护历史版本的一个数据结构
要查询区间第k大,自然就可以想到维护\(1-i\)在这个区间\([l,r]\)里个数
为了简化问题,可以率先考虑区间\([1,k]\)里的数字,随后运用前缀和解决问题
但如果每次操作都保存一棵线段树,这样子空间肯定会爆掉(
所以我们用更为优雅的方法记录历史版本
观察发现,每次操作只会更新线段树上的一条链,所以我们可以只保存一条链,并且跟原来的一整棵线段树的一部分节点构建父子关系
这样一来,就可以大大降低空间的使用了
下面来几张图解释一下建树的过程
我们以\([25957,6405,15770,26287,26465]\)为例,先对他离散化,得到\([3,1,2,4,5]\)
先建一棵空树
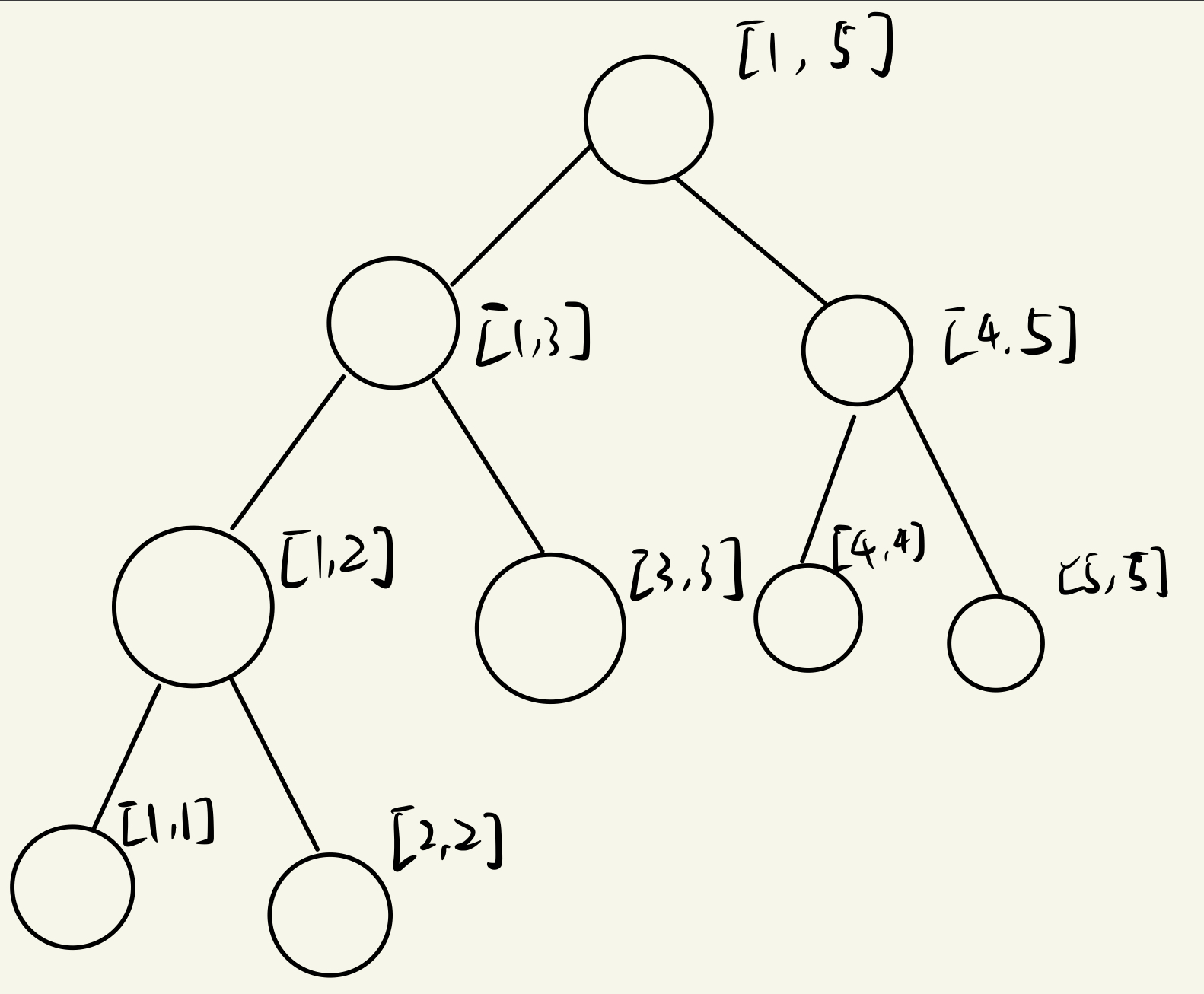 1
1
然后添加第一个节点,也就是离散化后的\('3'\)
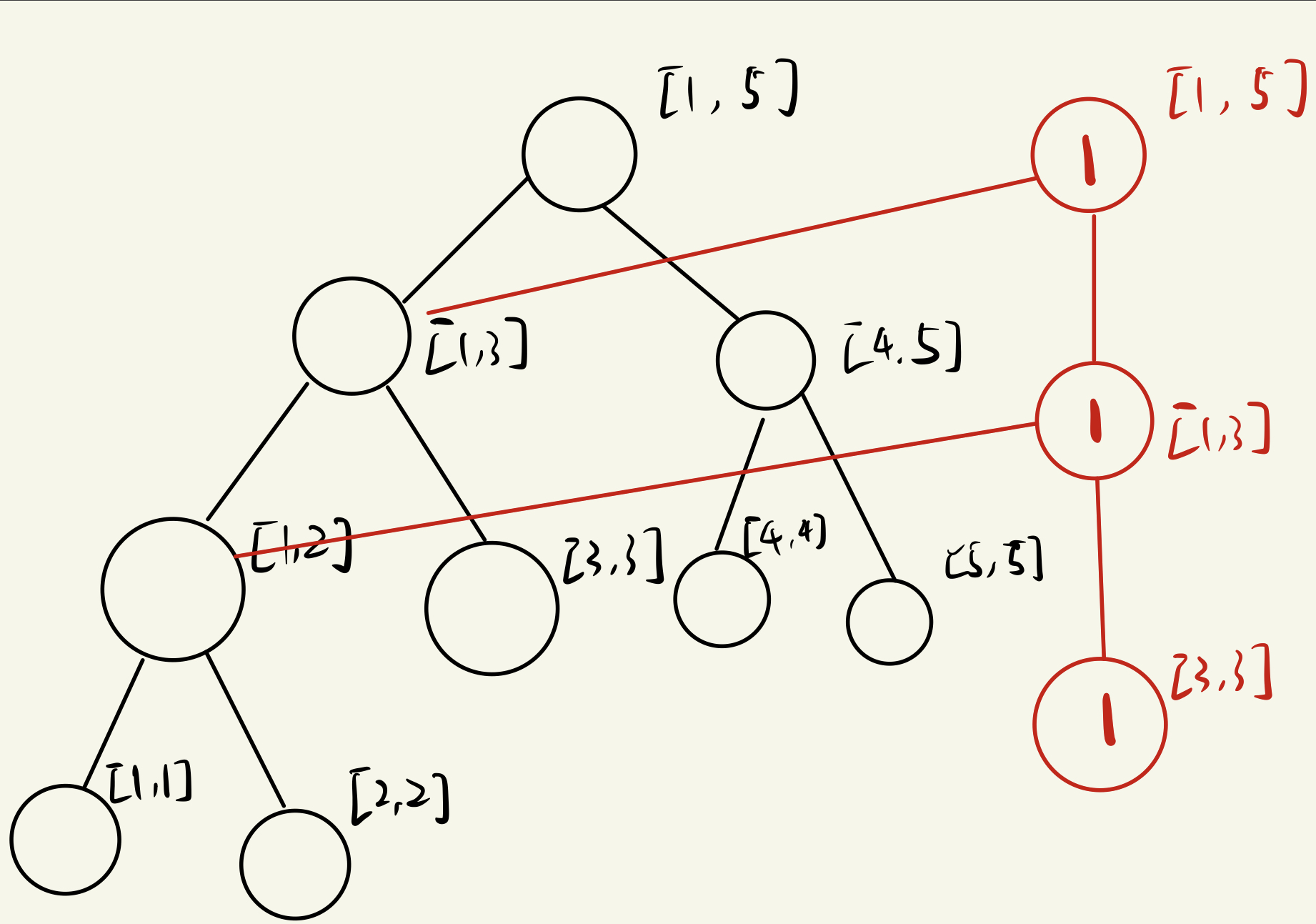 2
2
然后以此类推,最后的树长成这样
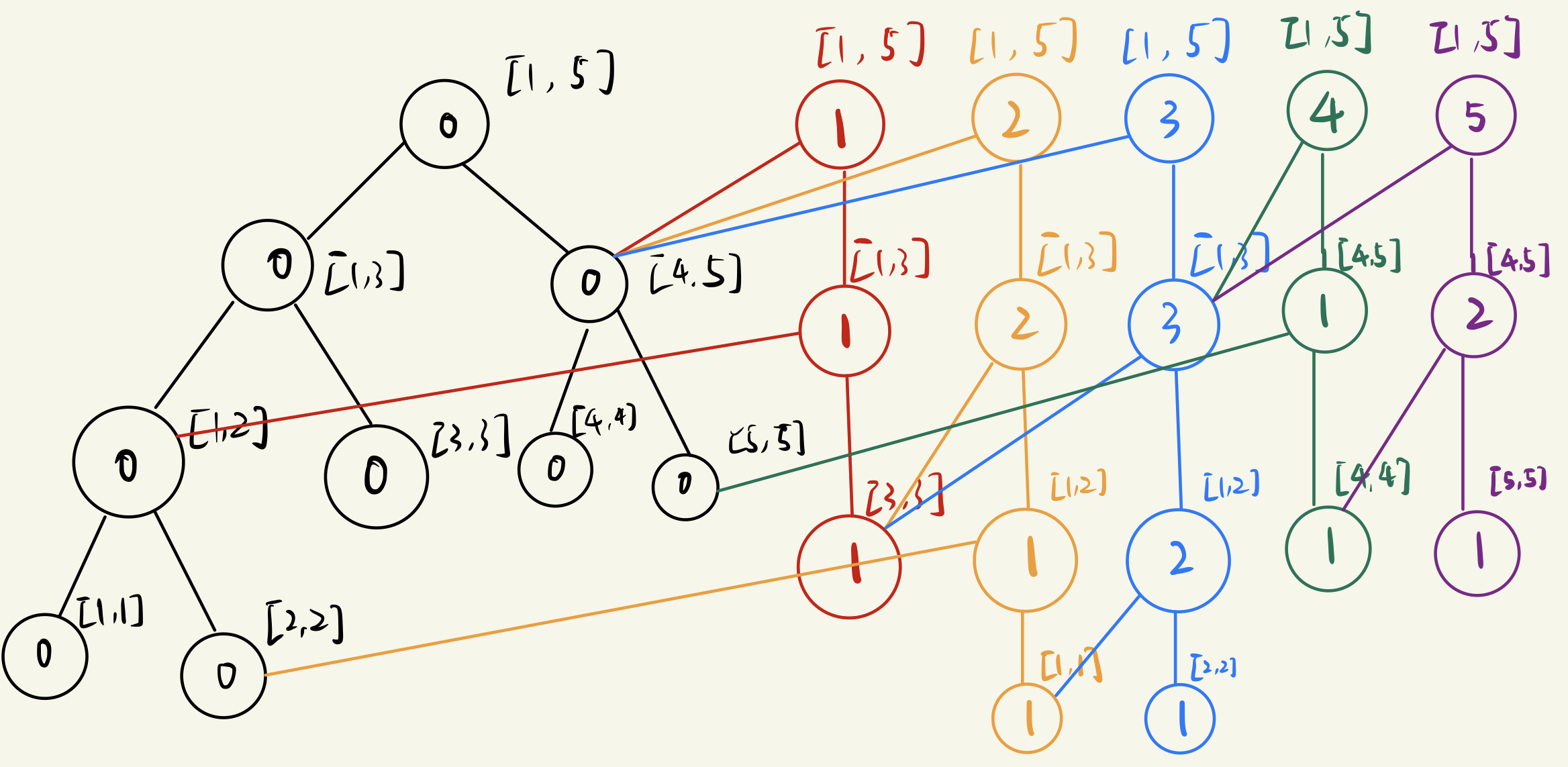 6
6
不同的颜色表示了不同的操作次数
显然,我们无法使用跟普通线段树类似的堆的方法存储节点的左右孩子,所以需要另外开两个数组存储
查询时,我们只需要对左子树做差,得到一个值\(x\),如果结果大于我们需要的\(k\),那就从右子树继续查询,但查询的值得减去\(x\);如果小于,就继续从左子树查询
代码如下
| int query(int ql, int qr, int l, int r, int k) {
int mid = (l + r) >> 1, x = sum[ls[qr]] - sum[ls[ql]];
if(l == r) return l;
if(k <= x) return query(ls[ql], ls[qr], l, mid, k);
else return query(rs[ql], rs[qr], mid + 1, r, k - x);
|
为了实现这个数据结构,我们还需要一个数组\(rt\)来存储每一棵线段树的根节点的信息,也就是上图中最上面的一层。
至此,我们已经悟了主席树是个什么东西和大概怎么实现,细节部分会在下面实现的代码中呈现
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| const int LOG = 20;
int n, m, len, tot;
int a[maxn], ind[maxn];
int sum[maxn * LOG], rt[maxn], ls[maxn * LOG], rs[maxn * LOG];
inline int getid(const int &val) {
return lower_bound(ind + 1, ind + 1 + len, val) - ind;
}
int build(int l, int r) {
int root = ++tot;
if(l == r) return root;
int mid = (l + r) >> 1;
ls[root] = build(l, mid);
rs[root] = build(mid + 1, r);
return root;
}
int update(int k, int l, int r, int root) {
int dir = ++tot;
ls[dir] = ls[root], rs[dir] = rs[root], sum[dir] = sum[root] + 1;
if(l == r) return dir;
int mid = (l + r) >> 1;
if(k <= mid) ls[dir] = update(k, l, mid, ls[dir]);
else rs[dir] = update(k, mid + 1, r, rs[dir]);
return dir;
}
int query(int ql, int qr, int l, int r, int k) {
int mid = (l + r) >> 1, x = sum[ls[qr]] - sum[ls[ql]];
if(l == r) return l;
if(k <= x) return query(ls[ql], ls[qr], l, mid, k);
else return query(rs[ql], rs[qr], mid + 1, r, k - x);
}
inline void init() {
n = read(), m = read();
rep(i, 1, n) a[i] = read();
memcpy(ind, a, sizeof(ind));
sort(ind + 1, ind + 1 + n);
len = unique(ind + 1, ind + 1 + n) - ind - 1;
rt[0] = build(1, len);
rep(i, 1, n) {
rt[i] = update(getid(a[i]), 1, len, rt[i - 1]);
}
}
inline void work() {
rep(i, 1, m) {
int l = read(), r = read(), k = read();
printf("%d\n", ind[query(rt[l - 1], rt[r], 1, len, k)]);
}
}
|
空间分析
我们一开始得先开一棵线段树,由于是动态开点,所需空间是\(2n-1\),在后续的更新操作中,每次操作最多需要\(\lceil logn\rceil +1\)个点
综上,我们总共需要\(2n-1+n(\lceil
logn\rceil +1)\)个点,瞎估估就是\(n(3+
\lceil logn\rceil)\)个节点
时间分析
我们开一棵空树需要的时间是\(O(logn)\),每次更新和查询的时间开销也是\(O(logn)\)的,对于m次查询,总共的时间复杂度就是\(O(mlogn)\)的
还是非常优秀的
写在最后
上面是我学习完主席树后的一点笔记,如果您发现了任何问题,请在下面评论直接告诉我(评论期望近期开放)


